Table of Contents
Data structure
Linear data structure
- 한 종류의 데이터가 선처럼 길게 나열된 자료구조
- 모든 자료에 O(1)으로 접근이 보장되는 자료구조에는 배열과 해시(key:value)가 있음
- 파이썬에서는 (배열=리스트), (해시=딕셔너리)
- 하단부터는 모든 자료에 O(1) 접근이 보장되지 않는 자료구조를 설명
Stack
먼저 들어간 자료가 나중에 나오는 자료구조 (후입선출)
자료를 넣는 push 함수와 자료를 빼는 pop 함수 (empty, full 등 ..)
시간 복잡도 (Time Complexity)
- push : O(1)
- pop : O(1)
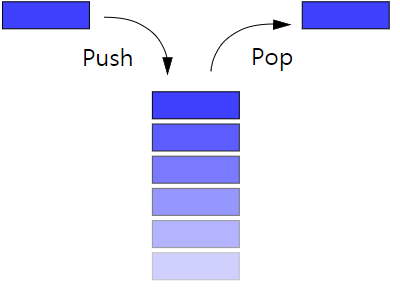
stack class
class stack: def __init__(self): self.items = [] def isEmpty(self): return self.items == [] def push(self, item): self.items.append(item) def peek(self): return self.items[-1] def size(self): return len(self.items) def pop(self): return self.items.pop() def reverseString(str): st = stack() result = "" for i in str: st.push(i) while st.isEmpty() != True: result += st.pop() return result if __name__ == "__main__": print(reverseString("Hello"))olleHstack 구현
class stack: def __init__(self): self.items = [] # pop def pop(self): item_length = len(self.items) # 스택이 비어있을 경우 if item_length < 1: print("Stack is empty!") return False # else 가장 위에 있는 item을 반환하며 삭제 result = self.items[item_length - 1] del self.items[item_length - 1] return result # push def push(self, x): self.items.append(x) # isEmpty def isEmpty(self): return not self.items if __name__ == "__main__": # test test = stack() test.push(1) test.push(3) test.push(5) print(test.items) print(test.pop()) print(test.pop()) print(test.pop()) print(test.isEmpty())[1, 3, 5] 5 3 1 True
Queue
먼저 들어간 자료가 먼저 나오는 자료구조 (선입선출)
자료를 넣는 Enquueu 함수와 자료를 빼는 Dequeue 함수
시간 복잡도 (Time Complexity)
- enqueue : O(1)
- dequeue : O(N)
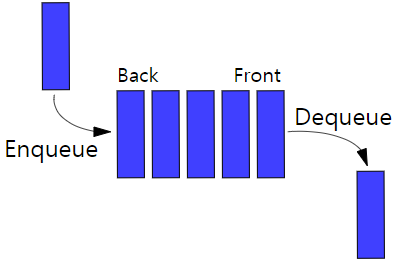
Queue class
class queue: def __init__(self): self.items = [] def enqueue(self, item): self.items.insert(0, item) def dequeue(self): return self.items.pop() def isEmpty(self): return self.items == [] def size(self): return len(self.items) if __name__ == "__main__": test = queue() test.enqueue(1) test.enqueue(3) test.enqueue(5) print('size : ', test.size()) print(test.dequeue()) print(test.dequeue()) print(test.dequeue()) print(test.isEmpty())size : 3 1 3 5 TrueQueue 구현
class queue(): def __init__(self): self.item = [] def dequeue(self): if len(self.item) == 0: return -1 return self.item.pop(0) def enqueue(self, n): self.item.append(n) pass def printQueue(self): print(self.item)
Deque
- stack가 queue의 융합
- 양쪽 끝에서 삽입과 삭제가 모두 가능
- 보통 입력이나 출력 중 하나를 한 쪽 입구만 가능하게 제한하는 형태가 많이 쓰임
Hash
- Key-value 쌍으로 데이터를 저장하는 자료구조
- 빠른 검색 속도
- Hash Table에 Hash를 저장
Linked list
(= 연결 리스트), 값과 다음 노드를 가짐
중간에서 삽입 삭제 가능
원소들이 흩어져있어 구현체의 속도가 느리기 때문에 잘 사용되지는 않는 편
# Node class Node(object): def __init__(self, data): self.data = data self.next = None # Singly linked list class LinkedList(): def __init__(self): self.head = None self.tail = None # Add new node at the end of the linked list def enqueue(self, node): if self.head == None: self.head = node self.tail = node else: self.tail.next = node self.tail = self.tail.next def dequeue(self): if self.head == None: return -1 v = self.head.data self.head = self.head.next if self.head == None: self.tail = None return v # print def print(self): obj = self.head string = "" while obj: string += str(obj.data) if obj.next: string += " -> " obj = obj.next print(string) if __name__ == "__main__": list = LinkedList() # Add object list.enqueue(Node(1)) list.enqueue(Node(2)) list.enqueue(Node(3)) list.enqueue(Node(4)) list.print() # 1->2->3->4 # Delete object print(list.dequeue()) print(list.dequeue()) list.print() # 3->41 -> 2 -> 3 -> 4 1 2 3 -> 4
선형 구조의 자료 탐색법
순차 탐색
- 시작점부터 순차적으로 탐색
- 모든 데이터를 탐색할 경우 O(n)
이분 탐색
순차 탐색보다 더 빠르속도를 기대, O(log2N)
중간값에서 시작하여 매번 일정한 조건에 따라 어떤 방향의 중간값으로 탐색할지 결정
특수한 기준으로 정렬되어있는 상태에서 사용 가능
import math def binarySearch(arr, n): start = 0 end = len(arr)-1 while end-start >= 0: mid = math.ceil((start+end)/2) # 어떤 방향의 중간값으로 탐색할지 결정 if arr[mid]==n: return mid+1 if arr[mid]<n: start = mid+1 else: end = mid-1 return -1; if __name__ == "__main__": arr = [1,3,4,6,7,9,13,15] num = 3 print(binarySearch(arr, num))2
Nonlinear data structure
- 선형 자료구조가 아닌 모든 자료구조
Graph
- 객체들 사이의 관계를 정점(vertex)과 간선(edge)로 나타낸 그림
DFS
Depth First Search (깊이 우선 탐색)
방문한 정점으로부터 깊게 들어가며 탐색한 후, 되돌아 나오다가 탐색하지 않은 노드를 탐색하는 방식
깊이가 너무 Depth가 너무 큰 경우, 런타임 에러 발생 우려
실행 과정
- 정점을 방문
- 인접한 정점 중 아직 방문하지 않은 정점을 방문(한 길로 쭉 파고 들어간다)
- 더 이상 들어갈 길이 없을 때(인접한 모든 정점이 이미 방문한 정점일 때), 방문하지 않은 인접한 정점을 찾을 때까지 들어간 길을 돌아나옴
- 위 과정을 반복
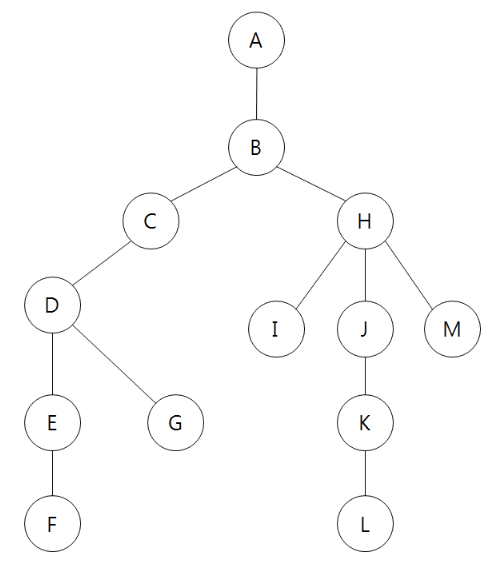
def dfs(v): # 정점 v부터 탐색 global rst if v == 'A': visited[v] = True rst += v + ' -> ' for i in Graph[v]: if not visited[i]: visited[i] = True rst += i + ' -> ' dfs(i) if __name__ == "__main__": Graph = { 'A': ['B'], 'B': ['A', 'C', 'H'], 'C': ['B', 'D', 'G'], 'D': ['C', 'E'], 'E': ['D', 'F'], 'F': ['E'], 'G': ['D'], 'H': ['B', 'I', 'J', 'M'], 'I': ['H'], 'J': ['H', 'K'], 'K': ['J', 'L'], 'L': ['K'], 'M': ['H'] } visited = dict(zip([v for v in Graph], [False for _ in Graph])) # 방문 여부 체크 rst = '' dfs('A') print(visited) print(rst){'A': True, 'B': True, 'C': True, 'D': True, 'E': True, 'F': True, 'G': True, 'H': True, 'I': True, 'J': True, 'K': True, 'L': True, 'M': True} A -> B -> C -> D -> E -> F -> G -> H -> I -> J -> K -> L -> M
BFS
Breadth First Search (너비 우선 탐색)
넓게 퍼져가며 정점을 방문
실행 과정
- 첫 정점을 방문
- 아직 방문하지 않은 인접한 정점들을 큐에 넣음
- 큐에 있는 정점들을 순서대로 방문
- 큐에 있는 정점에 대해 인접하면서 아직 방문하지 않은 정점들로 새로운 큐를 구성
- 위 과정을 반복

def bfs(v): global rst visited[v] = True queue = [v] while queue: now = queue.pop(0) rst += now + ' -> ' for i in Graph[now]: if not visited[i]: visited[i] = True queue.append(i) if __name__ == "__main__": Graph = { 'A': ['B'], 'B': ['A', 'C', 'H'], 'C': ['B', 'D', 'G'], 'D': ['C', 'E'], 'E': ['D', 'F'], 'F': ['E'], 'G': ['D'], 'H': ['B', 'I', 'J', 'M'], 'I': ['H'], 'J': ['H', 'K'], 'K': ['J', 'L'], 'L': ['K'], 'M': ['H'] } visited = dict(zip([v for v in Graph], [False for _ in Graph])) rst = '' bfs('A') print(visited) print(rst){'A': True, 'B': True, 'C': True, 'D': True, 'E': True, 'F': True, 'G': True, 'H': True, 'I': True, 'J': True, 'K': True, 'L': True, 'M': True} A -> B -> C -> H -> D -> G -> I -> J -> M -> E -> K -> F -> L
Tree
- 그래프의 일종
- 정점(node)과 간선(branch)로 이루어짐
- 2진 트리 : 모든 노드의 차수가 2 이하인 트리
- 전 이진 트리 : 모든 노드의 차수가 0 또는 2인 트리
- 포화 이진 트리 : 모든 단말 노드의 깊이가 같은 이진 트리.
- 완전 이진 트리 : 모든 단말 노드의 깊이의 최댓값과 최솟값의 차이가 0 또는 1인 이진 트리
- 트리 순회 알고리즘
- 전위 순회
- 중위 순회
- 후위 순회
Binary Search Tree
일자로 나열된 정렬된 데이터에서 원하는 데이터를 빠르게 찾는 방법
구성
- 일렬로 나열된 데이터들 중 가장 중앙에 위치한 하나의 데이터를 M이라고 하고, M 왼쪽에 위치한 데이터들을 L, 오른쪽에 위치한 데이터를 R 이라고 가정
- L과 R이 M을 부모로 가지는 트리를 구성
- L과 R에 대해서도 각각 같은 방법으로 트리를 구성
이진 검색
이분 탐색과 동일한 알고리즘
이진 검색 트리의 루트 노드부터 방문하며, 다음 순서에 따라 노드를 방문
과정
방문한 노드가 찾는 값이라면 검색 성공
방문한 노드가 단말노드이고 찾는 값이 아니라면 검색 실패
방문한 노드가 단말노드가 아니고 찾는 노드가 아니면
방문한 노드의 값을 x, 찾는 값을 v라고 할 때, x < v
-방문한 노드의 오르쪽 자식을 방문
x > v
-방문한 노드의 왼쪽 자식을 방문
Sorting Algorithm
Bubble Sort
거품정렬
인접한 두 개의 원소를 비교하여 자리를 교환하는 방식
- 첫 번째 원소부터 마지막 원소까지 반복하여 한 단계가 끝나면 가장 큰 원소가 마지막 자리로 정렬
구현이 간단하지만 비효율적
time complexity
- Best : O(n2)
- Average : O(n2)
- Worst : O(n2)
def bubbleSort(x): length = len(x)-1 for i in range(length): for j in range(length-i): if x[j] > x[j+1]: x[j], x[j+1] = x[j+1], x[j] return x if __name__ == "__main__": arr = [7, 9, 2, 10, 3, 8, 1, 4, 5, 6] rst = bubbleSort(arr) print(rst)[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Selection Sort
선택정렬
전체 원소들 중 기준 위치에 맞는 원소를 선택하여 자리를 교환하는 방식
- 전체 원소 중 가장 작은 원소를 찾아 선택하여 첫 번째 원소와 교환
- 그 다음 두 번째 작은 원소를 찾아 선택하여 두 번째 원소와 교환
- 이 과정을 반복
구현이 간단하지만 비효율적
time complexity
- Best : O(n2)
- Average : O(n2)
- Worst : O(n2)
def selectionSort(x): length = len(x) for i in range(length-1): for j in range(i+1, length): if x[i] > x[j]: x[i], x[j] = x[j], x[i] return x if __name__ == "__main__": arr = [7, 9, 2, 10, 3, 8, 1, 4, 5, 6] rst = selectionSort(arr) print(rst)[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Insertion Sort
삽입정렬 (Insertion Sort)
정렬되어 있는 부분집합에 정렬할 새로운 원소의 위치를 삽입하는 방식 -정렬된 부분집합(S), 정렬할 부분집합(U)
- 정렬되지 않은 U의 원소를 하나씩 꺼내서 이미 정렬되어있는 S의 마지막 원소부터 비교하면서 위치를 찾아 삽입
- 삽입 정렬이 반복되며 S의 원소는 하나씩 늘고, U의 원소는 하나씩 감소
- U가 공집합이 되면 정렬이 완성
구현이 간단하지만 비효율적
- 정렬된 데이터에 새 값을 하나 넣을 때, 빠른 효능
- 적은 데이터에 사용하기에 괜찮은 정렬 알고리즘
time complexity
- Best : O(n)
- Average : O(n2)
- Worst : O(n2)
def insertSort(x): for i in range(1, len(x)): j = i - 1 key = x[i] while x[j] > key and j >= 0: x[j+1] = x[j] j = j - 1 x[j+1] = key return x if __name__ == "__main__": arr = [7, 9, 2, 10, 3, 8, 1, 4, 5, 6] rst = insertSort(arr) print(rst)[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Merge Sort
병합 정렬 (Merge Sort)
2개 이상의 자료를 오름차순이나 내림차순으로 재 배열하는 것(여러 개의 정렬된 자료의 집합을 병합하여 한 개의 정렬된 집합으로 정렬)
부분집합으로 분할(divide), 각 부분집합에 대해서 정렬 작업을 완성(conquer) 한 후, 정렬된 부분집합들을 다시 결합(combine)하는 분할 정복(divide and conquer) 기법 사용
n-way 병합 : n 개의 정렬된 자료의 집합을 결합하여 하나의 집합으로 만드는 병합 방법
- 분할(divide) : 입력 자료를 같은 크기의 부분집합 2개로 분할
- 정복(conquer) : 부분집합의 원소들을 정렬. 부분집합의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 기법을 적용
- 결합(combine) : 정렬된 부분집합들을 하나의 집합으로 결합
- 1, 2, 3의 과정을 반복 수행하면서 정렬을 완성
복잡하지만 효율적
time complexity
- Best : O(nlog2n)
- Average : O(nlog2n)
- Worst : O(nlog2n)
def mergeSort(x): # 집합의 원소가 1개 남았을 경우 해당 원소 반환 if len(x) <= 1: return x # 분할(divide), 정복(conquer) 단계 m = len(x) // 2 L = mergeSort(x[:m]) R = mergeSort(x[m:]) # 결합(combine) 단계 result = [] i = 0 j = 0 while i < len(L) and j < len(R): if L[i] < R[j]: result.append(L[i]) i += 1 else: result.append(R[j]) j += 1 result += L[i:] result += R[j:] return result if __name__ == "__main__": arr = [7, 9, 2, 10, 3, 8, 1, 4, 5, 6] rst = mergeSort(arr) print(rst)[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Quick Sort
퀵정렬 (Quick Sort)
정렬할 전체 원소에 대해서 정렬을 수행하지 않고, 기준 값을 중심으로 왼쪽 부분 집합과 오른쪽 부분 집합으로 분할하여 정렬하는 방식 (기준값은 pivot, 일반적으로 전체 원소 중 가운데 위치한 원소를 선택)
- 왼쪽 부분 집합에는 기준 값보다 작은 원소들을 이동시키고, 오른쪽 부분 집합에는 기준 값보다 큰 원소들을 이동
- 분할(divid) : 정렬할 자료들을 기준 값 중심으로 2개의 부분집합으로 분할
- 정복(conquer) : 부분집합의 원소들 중에서 기준 값보다 작은 원소들은 왼쪽 부분집합으로, 기준 값보다 큰 원소들은 오른쪽 부분집합으로 정렬
- 부분집합의 크기가 1이하로 충분히 작지 않으면 순환 호출을 이용하여 다시 분할
O(nlog2n) 알고리즘들 중 가장 빠름
time complexity
- Best : O(nlog2n)
- Average : O(nlog2n)
- Worst : O(n2)
def quicksort(x): if len(x) <= 1: return x # 분할(divide) pivot = x[len(x) // 2] less = [] more = [] equal = [] # 정복(conquer) for a in x: if a < pivot: less.append(a) elif a > pivot: more.append(a) else: equal.append(a) return quicksort(less) + equal + quicksort(more) if __name__ == "__main__": arr = [7, 9, 2, 10, 3, 8, 1, 4, 5, 6] rst = quicksort(arr) print(rst)[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Shell Sort
- 셸 정렬 (Shell Sort)
- 일정한 간격으로 떨어져있는 자료들끼리 부분집합을 구성(간격별 비교)하고 각 부분집합에 있는 원소들에 대해 삽입 정렬을 수행하는 작업을 반복하는 방식 (전체 원소에 대해서 삽입 정렬을 수행하는 것보다 부분집합으로 나누어 삽입 정렬을 하게 되면 비교적 비교 연산과 교환 연산이 감소할 수 있는 점에서 착안)
- 부분집합의 기준이 되는 간격을 interval에 저장
- 한 단계가 수행될 따마다 interval의 값을 감소시키고 쉘 정렬을 순환 호출
- invertal가 1이 될 때까지 반복 (interval 값은 보통 원소 개수의 1/2로 사용)
time complexity
- Best : O(n)
- Average : O(n1.5)
- Worst : O(n2)
Heap Sort
- 힙 정렬 (Heap Sort)
- 최대 힙 트리나 최소 힙 트리를 구성해 정렬하는 방법 (내림차순 정렬 : 최대 힙, 오름차순 정렬 : 최소 힙을 구성)
- n개의 노드에 대한 완전 이진 트리를 구성, 이때 루트 부노드, 왼쪽 자노드, 오른쪽 자노드 순으로 구성
- 최대 힙(부노드가 자노트보다 큰 트리) 구성, 아래부터 루트까지 올라오며 순차적으로 정렬
- m번째 정렬이 끝이 나면 가장 큰 수(루트에 위치)를 마지막 노드와 교환, 여기서 가장 큰 수는 트리에서 나옴
- 2, 3의 과정을 반복
- 복잡하지만 효율적
- time complexity
- Best : O(nlog2n)
- Average : O(nlog2n)
- Worst : O(nlog2n)
- time complexity
Radix Sort
- 기수 정렬
- 원소의 키값을 나타내는 기수를 이용한 정렬
- 정렬할 원소의 키값에 해당하는 버킷에 원소를 분배하였다가 버킷의 순서대로 원소는 꺼내는 방법을 반복하면서 정렬
- 키값의 일의 자리에 대해서 기수 정렬을 수행
- 다음 단계에서는 키값의 십의 자리에 대해서 정렬을 수행
- 그리고 그다음 단계에서는 백의 자리에 대해서 정렬을 수행
- 1, 2, 3에서 진행되었던 것처럼 자릿수만큼 반복하여 정렬을 수행
- 복잡하지만 효율적