Table of Contents
Numerical analysis
- 수치 해석 : 직접 풀기 힘든 수학 문제를 근사적으로 푸는 알고리즘과 이들의 수치적 안정성, 오차의 범위 등으 연구하는 전산학의 한 분야
bisection method
- 이분법 : 가장 유용하게 사용되는 수치 해석 기법
- 주어진 범위 [lo, hi] 내에서 어떤 함수 f(x)의 값이 0이 되는 지점을 수치적으로 찾아내는 기법
- 단조 함수(주어진 순서를 보존하는 함수)가 아니고, 답이 여러 개 있는 함수라도 연속이기만 하다면 이분법을 사용해 근을 찾을 수 있음
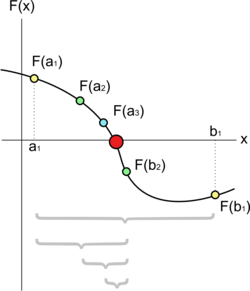
- 이분법 사용을 위해 우선 함수의 그래프 상에서 x축 윗부분에 위치한 점 하나와 아랫부분에 위치한 점 하나를 찾아야 함 -> 여기서 (lo, f(lo)) 와 (hi, f(hi)) 가 적당한 후보
- 이분법은 매 반복마다 [lo, hi] 구간의 크기를 절반으로 줄여 나아감
double f(double x); // 이분법 예제 구현 double bisection(double lo, double hi) { // 반복문 불변식을 강제 if(f(lo) > 0) swap(lo, hi); // 반복문 불변식 : f(lo) <= 0 < f(hi) // 반복문 불변식을 강제하기 위해 lo > hi 가 될 수 있으므로 (hi-lo)는 절대값 while(fabs(hi - lo) > 2e-7) { double mid = (lo + hi) / 2; double fmid = f(mid); // 두 부분 구간 중 어느 쪽을 선택해야할지 결정 if(fmid <= 0) lo = mid; else hi = mid; } // 중간 값 반환(최대 오차를 최소화할 수 있는 답이 중간 값이므로) return (lo + hi) / 2; }- f(lo) 와 f(hi) 의 부호가 다르다는 조건 대신 f(lo) 는 항상 0 이하이고 f(hi) 는 항상 양수라는 반복문 불변식을 유지
- 절대 오차를 이용한 종료 판정 : hi 와 lo 의 절대 오차를 이용한 반복문의 종료 판정을 구현 -> hi 와 lo 가 충분히 가까워질 경우 [lo, hi] 구간 내에서 임의의 답을 선택하여 반환
- 상대 오차를 이용한 종료 판정 : 절대 오차를 사용하는 방법은 다루는 값의 크기가 작을 때는 훌륭하지만 값의 크기가 커지면 문제가 발생 -> 알고리즘 문제에서는 이러한 문제 때문에 절대 오차 외에도 상대 오차를 허용
- 초기 lo, hi 설정
- a 를 lower, b 를 upper 라고 했을 때,
- 구간 [a, b]에 속해있는 c는 다음을 만족
f(a) <= f(c) <= f(b)혹은f(a) >= f(c) >= f(b) - lower 를 0 으로 잡고 증가시키면서 f(a) 가 음수에서 양수로 바뀌는 지점을 찾는다.
- 만일 f(2) < 0, f(3) > 0 라면 lower 는 2, upper 는 3.
Ternary Search
- 삼분 탐색
함수에서 극값, 최대/최소값을 찾을 때 유용하게 사용할 수 있는 기법
이분법이 매 반복마다 답의 후보 구간을 절반으로 자르는 것과 비슷하게, 답의 후보 구간을 삼등분하는 두 위치에서 함수의 값을 계산
- 세 가지 조건을 만족하는 함수에 사용 가능
- 지역 극대점(local maximum), 하나의 극대(mode)가 있는 유니모달 함수(unimodal function)
- 최대점 왼쪽은 순증가(strictly increasing)
- 최대점 오른쪽은 순감소(strictly decreasing)
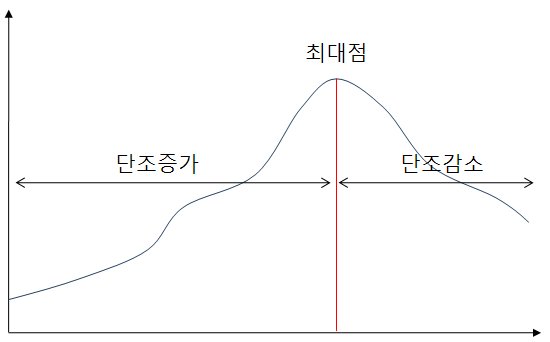
삼분 검색을 사용하기 위해 이분법과 비슷하게 최대치를 포함하는 후보 구간을 우선 알고 있어야 함
이 구간을 [lo, hi] 라고 할 경우, 구간의 삼등분 위치는 각각 (2 lo + hi / 3), (lo + 2 hi / 3)
lo = 120, hi = 230 이라고 할경우 삼등분 위치는 (156.666초, 193.666초)
이 두 값 중 오른쪽 값이 더 크므로 1/3 구간인 [lo, (2 lo + hi / 3)] 에는 최대치가 있을 수 없음 -> 이 구간에 최대치가 있다면 그 오른쪽 부분은 순감소 해야함
따라서 답이 존재할 수 있는 구간을 [(2 lo + hi / 3), hi] 로 줄일 수 있게 됨 -> 이처럼 삼분 검색은 한 번 반복할 때마다 후보 구간의 크기를 2/3으로 줄여나감
// 최대치를 찾고 싶어하는 함수 double f(double x); // [lo, hi] 구간에서 f(x)가 최대치를 갖는 x 를 반환 double ternary(double lo, double hi) { for(int iter = 0; iter < 100; iter++) { double a = (2*lo + hi) / 3.0; double b = (lo + 2*hi) / 3.0; if(f(a) > f(b)) hi = b; else lo = a; } return (lo + hi) / 2.0; }- 입력의 정의를 간단히 바꾸면 삼분 검색은 최소치를 찾는 데도 쓸 수 있음 -> 지역 극소점이 하나밖에 없고, 이 점 왼쪽으로는 순감소, 오른쪽으로는 순증가하는 함수가 있다면 똑같이 삼분 검색을 사용할 수 있음
// 할 생각이 있는 최대 게임 수 long long L = 2000000000; // b 게임 중 a 게임 승리했을 때의 승률 int ratio(long long b, long long a) { return (a * 100) / b; } // 최소 몇 연승해야 승률이 올라갈지 int neededGames(long long games, long long won) { // 불가능한 경우(L 번 게임을 더 해도 승률이 올라가지 않는 경우) if(ratio(games, won) == ratio(games + L, won + L)) return -1; long long lo = 0, hi = L; // 반복문 불변식 : // 1. lo 게임 이기면 승률은 변하지 않는다. // 2. hi 게임 이시면 승률은 변한다. while(lo + 1 < hi) { long long mid = (lo + hi) / 2; // mid 번 게임을 더 해도 승률이 더 오르지 않는 경우 if(ratio(games, won) == ratio(games + mid, won + mid)) lo = mid; else hi = mid; } return hi; }수학적 해법
- 승률 R이 되는 최소 연승 수 x에 대한 식 구하기
- floor( (100 (M+x)) / (N + x) ) >= R
- 100 M + 100 x >= R (N + x)
- (100 - R) x >= R N - 100 M
- x >= ceil( (R N - 100 M) / (100 - R) )
- 승률 R이 되는 최소 연승 수 x에 대한 식 구하기
Number theory
- 정수론
소수 판별
합성수 n 이 p x q 로 표현될 때 한 수는 항상 sqrt(n) 이하, 다른 한 수는 항상 sqrt(n) 이상이라는 점을 이용하면 n-1 까지 순회하지 않고 sqrt(n) 까지만 순회하도록 최적화 가능, O(sqrt(n))
- prime number : 소수는 양의 약수가 1과 자기 자신 두 개 뿐인 자연수
- composite number : 합성수는 세 개 이상의 양의 약수를 갖는 자연수
// 주어진 자연수 n 이 소수인지 확인 bool isPrime(int n){ // 예외 처리 : 1과 2는 예외로 처리 if(n <= 1) return false; if(n == 2) return true; // 2를 제외한 모든 짝수는 소수가 아님 if(n % 2 == 0) return false; // 2를 제외했으니 3이상의 모든 홀수로 나누기 int sqrtn = int(sqrt(n)); for(int div = 3; div <= sqrtn; div += 2) if(n % div == 0) return false; }
소인수 분해(prime factorization)
소인수 분해는 한 합성수를 소수들의 곱으로 표현하는 방법
//주어진 정수 n을 소인수분해 vector<int> factor(int n){ vector<int> ret; int sqrtn = int(sqrt(n)); for(int div = 2; div <= sqrtn; div++) while(n % div == 0) { n /= div; ret.push_back(div); } if(n > 1) ret.push_back(n); return ret; }
에라토스테네스의 체(Sieve of Eratosthenes)
지워지지 않은 수를 찾을 때 n이 아니라 sqrt(n) 까지만 탐색하여 최적화
i 의 배수들을 모두 지울 때, 2 x i 에서 시작하는 것이 아니라 i x i 에서 시작
int n; bool isPrime[MAX_N + 1]; void eratosthenes() { memset(isPrime, 1, sizeof(isPrime)); // 1은 항상 예외처리 isPrime[0] = isPrime[1] = false; int sqrtn = int(sqrt(n)); for(int i = 2; i <= sqrtn; i++){ // 아직 지워지지 않았다면 if(isPrime[i]) // i 의 배수 j 들에 대해 isPrime[j] = false // i * i 미만의 배수는 이미 지워졌으므로 생략 for(int j = i * i; j <= n; j += i) isPrime[j] = false; } }수행 시간이 빠르지만 메모리 사용량이 큰 단점
많은 수에 대해 사용할 경우 짝수를 별도로 처리해서 필요한 배열의 크기를 절반으로 줄이거나, 비트마스크를 이용하는 등의 기법을 이용해 메모리 양을 최적화
- 에라토스테네스의 체는 여러 형태로 변형할 수 있으므로 여러 정수론 문제를 푸는 데 가장 유용하게 사용
Computational geometry
- 계산 기하 알고리즘 : 점, 선, 다각형과 원 등 각종 기하학적 도형을 다루는 알고리즘
- 벡터의 구현
- vector : 방향과 거리의 쌍, 방향과 거리를 모두 알고 있으면 두 점 사이의 상대적인 위치를 정확히 표시할 수 있음, 벡터의 직관적인 표현은 화살표
- 두 벡터 a, b 의 연산
- a + b : b 의 시작점을 a 의 끝점으로 옮겼을 때 b 의 끝점에서 끝나는 벡터
- a - b : b 의 끝점에서 a 의 끝점으로 가는 벡터
- a * r : a 의 길이를 r 배로 늘린 벡터
const double PI = 2.0 * acos(0.0); // acos(0.0) = 1.57079633... // 2차원 벡터 표현 struct vector2{ double x, y; // 생성자를 explicit 으로 지정하면 vector2를 넣을 곳에 실수가 들어가는 일을 방지 explicit vector2(double x_ = 0, double y_ = 0) : x(x_), y(y_) {} // 두 벡터의 비교 bool operator = (const vector2& rhs) const { return x == rhs.x && y == rhs.y; } bool operator < (const vector2& rhs) const { return x != rhs.x ? x < rhs.x : y < rhs.y; } // 벡터의 덧셈과 뺄셈 vector2 operator + (const vector2& rhs) const { return vector2(x + rhs.x, y + rhs.y); } vector2 operator - (const vector2& rhs) const { return vector2(x - rhs.x, y - rhs.y); } // 실수로 곱셈 vector2 operator * (double rhs) const { return vector2(x * rhs, y * rhs); } // 벡터의 길이 반환 double norm() const { return hypot(x, y); } // 방향이 같은 단위 벡터(unit vector2) 반환, 영벡터에 대해 호출한 경우 반호나 값은 정의되지 않음 vector2 normalize() const { return vector2(x / norm(), y / norm()); } // 벡터의 극 각도 // x 축의 양의 방향으로부터 이 벡터까지 반시계방향으로 잰 각도 double polar() const { return fmod(atan2(y, x) + 2 * PI, 2 * PI); } // 참고. https://mrw0119.tistory.com/12 // 내적(Inner product, Scalar product or Dot product) // 벡터의 사이각 구하기, 벡터의 직각 여부 확인, 벡터의 사영에 흔히 사용 double dot(const vector2& rhs) const { return x * rhs.x + y * rhs.y; // 좌표값의 각 성분을 곱해서 더하기 } // 외적 구현(Outer product or Cross product) // 두 개의 3차원 벡터에 대해 정의되는 연산, 3차원 벡터 a, b 가 주어졌을 때 이 두 벡터에 모두 수직인 다른 벡터를 반환 // 면접 계산, 두 벡터의 방향 판별에 흔히 사용 double cross(const vector2& rhs) const { return x * rhs.y - x * rhs.y; } // 벡터의 사영(vector projection) : 벡터 b 에 수직으로 빛이 내리쬘 때, 벡터 a 가 b 위에 드리우는 그림자 // 이 벡터를 rhs 에 사영한 결과 vector2 project(const vector2& rhs) const { vector2 r = rhs.normalize(); return r * r.dot(*this); } // 세 개의 점 p, a, b 가 주어졌을 때 a 가 b 보다 p 에 얼마나 더 가까운지 반환 double howMuchCloser(vector2 p, vector a, vector b) { return (b - p).norm() - (a - p).norm(); } // 두 벡터의 방향성을 판단하는 함수(Counter ClockWise) // 원점에서 벡터 b 가 벡터 a 의 반시계 방향이면 양수, 시계 방향이면 음수, 평행이면 0 을 반환 double ccw(vector2 a, vector2 b) { return a.cross(b); } // 점 p 를 기준으로 벡터 b 가 벡터 a 의 반시계 방향이면 양수, 시계 방향이면 음수, 평행이면 0을 반환 double ccw(vector2 p, vector2 a, vector2 b) { return ccw(a-p, b-p); } }
교차와 거리, 면적
- 직선의 교차를 작성할 수 있는 간단한 방법은 직선을 한 점과 방향 벡트, 즉 a + p.b(내적) 형태로 표현하는 방법
- a + p.b 와 c + p.d 의 교점을 구하기 위해 a + p.b = c + p.d 방정식을 풀면 가능
- p = ((c-a) X d) / (b X d)(외적)
// 두 직선의 교차점을 계산, 참고 : https://bowbowbow.tistory.com/17 // (a, b)를 포함하는 선과 (c, d)를 포함하는 선의 교점을 x 에 반환 // 두 선이 평행이면 (겹치는 경우를 포함) 거짓을, 아니면 참을 반환 bool lineIntersection(vector2 a, vector2 b, vector2 c, vector2 d, vector2& x) { double det = (b - a).cross(d - c); // 두 선이 평행이 경우, 분모가 0 if(fabs(det) < EPSILON) return false; x = a + (b - a) * ((c - a).cross(d - c) / det); return true; }
선분과 선분의 교차
Dynamic Programming
- 동적 계획법
- 문제의 답을 여러 번 계산하는 대신 한 번만 계산하고 계산 결과를 재활용함으로써 속도의 향상를 꾀함
- 두 번 이상 반복 계산되는 부분 문제들의 답을 미리 저장함으로써 속도의 향상을 꾀하는 알고리즘 설계 기법
- 캐시(cache) : 이미 계산한 값을 저장해 두는 메모리의 장소
- 중복되는 부분 문제(overlapping subproblems) : 두 번 이상 계산되는 부분 문제
- 메모이제이션(memoization) : 함수의 결과를 저장하는 장소를 마련해 두고, 한 번 계산한 값을 저장해 뒀다 재활용하는 최적화 기법, 메모이제이션은 참조적 투명 함수의 경우에만 적용 가능
- 참조적 투명 함수(referential transparent function) : 입력이 고정되어 있을 떄, 그 결과가 항상 같은 함수
- 메모이제이션의 패턴
#include <iostream> using namespace std; int cache[2500][2500]; // a와 b는 [0, 2500) 구간 안의 정수 int someObsureFunction(int a, int b) { // 기저 사례를 처음으로 처리.ex) 입력 범위를 벗어난 경우 if (...) return ...; // (a,b)에 대한 답을 구한 적이 있으면 바로 반환 int& rst = cache[a][b]; if (rst != -1) return rst; // 답 계산 ...; return rst; } int main() { ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); // memset()함수를 이용하여 cache 배열을 초기화 memset(cache, -1, sizeof(cache)) }
- first. 주어진 문제를 (재귀적으로 해결하는) 완전 탐색을 이용하여 해결
const int MAX = 100; int n, board[MAX][MAX]; bool jump(int y, int x) { // 기저 사례 : 게임판 밖을 벗어난 경우 if (y >= n || x >= n) return false; // 기저 사례 : 마지막 칸에 도달한 경우 if (y == n - 1 && x == n - 1) return true; int jumpSize = board[y][x]; return jump(y + jumpSize, x) || jump(y, x + jumpSize); }
- second. 중복된 부분 문제를 한 번만 계산하도록 메모이제이션 적용
- 완전 탐색 과정에서 중복으로 연산이 되는 부분들이 있는데, 이미 해결된 부분 문제들의 결과를 cache에 저장해주면서(메모이제이션 적용) 중복된 연산을 줄여줄 수 있음
int n, board[MAX][MAX]; int cache[MAX][MAX]; bool jump_mmz(int y, int x) { // 기저 사례 : 게임판 밖을 벗어난 경우 if (y >= n || x >= n) return 0; // 기저 사례 : 마지막 칸에 도달한 경우 if (y == n - 1 && x == n - 1) return 1; // 메모이제이션 적용 int& rst = cache[y][x]; if (rst != -1) return rst; int jumpSize = board[y][x]; return rst = jump_mmz(y + jumpSize, x) || jump_mmz(y, x + jumpSize); }
#include <iostream> #include <string> int cache[101][101]; string W, S; bool matchMemoized(int w, int s) { int &ret = cache[w][s]; if (ret != -1) return ret; // W[w]와 S[s] 비교 while (s < S.size() && w < W.size() && (W[w] == '?' || W[w] == S[s])) { // 첫 한 글자씩 떼고 남은 문자열이 서로 대응되는지 재귀 호출로 탐색 return ret = matchMemoized(w + 1, s + 1); } // 더 이상 대응할 수 없으면 왜 while문이 끝났는지 확인 // 2. 패턴 끝에 도달 if (w == W.size()) return ret = (s == S.size()); // 4. *를 만나서 끝난 경우 : *에 몇 글자를 대응해야 할지 if (W[w] == '*') { if (matchMemoized(w + 1, s) || (s < S.size() && matchMemoized(w, s + 1))) // *에 아무 글자도 대응시키지 않을 것인지 || 한 글자를 더 대응시킬 것인지 결정 return ret = 1; } // 3. 이 외의 경우에는 모두 대응되지 않음 return ret = 0; }
전통적 최적화 문제
- 여러 개의 가능한 답 중 가장 좋은 답(최적해)을 찾아내는 문제
- 1) 완전 탐색 알고리즘 설계 -> 2) 최적 부분 구조 설계 -> 3) 메모이제이션 적용
- 최적화 문제 동적 계획법 레시피
- 1) 모든 답을 만들어 보고 그 중 최적해의 점수를 반환하는 완전 탐색 알고리즘을 설계
- 2) 전체 답의 점수를 반환하는 것이 아니라, 앞으로 남은 선택들에 해당하는 점수만을 반환하도록 부분 문제의 정의를 바꿈
- 3) 재귀 호출의 이볅에 이전의 선택에 관련된 정보가 있다면 꼭 필요한 것만 남기고 줄임. 문제에 최적 부분 구조가 성립할 경우 이전 선택에 관련된 정보를 완전히 없앨 수도 있음. 여기서 목표는 가능한 중복되는 부분 문제를 많이 만드는 것. 입력의 종륙라 줄어들 수록 더 많은 부분 문제가 중복되고, 메모이제이션을 최대한도로 활용 가능해짐
- 4) 입력이 배열이거나 문자열인 경우 가능하다면 적절한 변환을 통해 메모이제이션할 수 있도록 함
- 5) 메모이제이션을 적용
전체 경로의 최대 합이 아닌 부분 경로의 최대합을 반환
- 점화식 : path(y, x) = triangle’[y]’‘[x]’ + max( path(y+1, x), path(y+1, x+1) )
- 최적화 문제 동적 계획법 레시피에 적용
- 1) 모든 경로를 만들어보고 전체 합 중 최대치를 반환하는 완전 탐색 알고리즘을 설계
- 2) 설계한 완전 탐색 알고리즘이 전체 경로의 최대 합을 반환하는 것이 아니라, (y, x) 이후로 만난 숫자들의 최대 합을 반환하도록 바꿈
- 3) 이렇게 반환 값의 정의를 바꿨기 때문에 이저넹 한 선택에 대한 정보인 sum을 입력 받을 필요가 없어짐. 이 정보를 받을 필요가 없어진 것은 문제에 최적 부분 구조가 성립하기 때문
- 4) 불필요한 항목
- 5) 메모이제이션을 적용
const int MAX = 100; int n, triangle[MAX][MAX]; int cache2[MAX][MAX]; // (y,x) 위치부터 맨 아래줄까지 내려가면서 얻을 수 있는 최대 경로를 반환 int path(int y, int x) { // 기저 사례 : 맨 아래줄까지 도달 if(y == n - 1) return triangle[y][x]; int& ret = cache2[y][x]; if(ret != -1) return ret; return ret = max(path(y + 1, x), path(y + 1, x + 1)) + triangle[y][x]; }- 최대 부분 구조(optimal substructure) : 동적 계획법의 중요 요소, 어떤 문제와 분할 방식에 성립하는 조건, 각 부분 문제의 최적해만 있으면 전체 문제의 최적해를 쉽게 얻어낼 수 있을 경우 이 조건이 성립
#include<cstring> #include<iostream> #include<string> #include<vector> #include<limits> #include <algorithm> using namespace std; // 입력이 32비트 부호 있는 정수의 모든 값을 가질 수 있으므로 인위적인 최소값은 64비트여야 한다 const long long NEGINF = numeric_limits<long long>::min(); int n, m, A[100], B[100]; int cache[101][101]; // min(A[indexA], B[indexB]), max(A[indexA], B[indexB]) 로 시작하는 // 합친 증가 부분 수열의 최대 길이를 반환한다 // 단 A[indexA] != B[indexB] 라고 가정한다. int jlis(int indexA, int indexB) { // 메모이제이션 int& ret = cache[indexA + 1][indexB + 1]; if(ret != -1) return ret; // A[indexA], B[indexB] 가 이미 존재하므로 2개는 항상 있다. ret = 2; long long a = (indexA == -1 ? NEGINF : A[indexA]); long long b = (indexB == -1 ? NEGINF : B[indexB]); long long maxElement = max(a, b); // 다음 원소를 찾는다 for(int nextA = indexA + 1; nextA < n; ++nextA) if(maxElement < A[nextA]) ret = max(ret, jlis(nextA, indexB) + 1); for(int nextB = indexB + 1; nextB < m; ++nextB) if(maxElement < B[nextB]) ret = max(ret, jlis(indexA, nextB) + 1); return ret; } int main() { int cases; cin >> cases; for(int cc = 0; cc < cases; ++cc) { cin >> n >> m; for(int i = 0; i < n; i++) { cin >> A[i]; } for(int j = 0; j < m; j++) { cin >> B[j]; } memset(cache, -1, sizeof(cache)); cout << jlis(-1, -1) - 2 << endl; } }- 문제 추가
Greedy method
- 탐욕법
- 가장 직관적인 알고리즘 설계 패러다임 중 하나
- 원하는 답을 재귀 호출과 똑같이 여러 개의 조각으로 쪼개고, 각 단계마다 답의 한 부분을 만들어 간다는 점에서 완전 탐색이나 동적 계획법 알고리즘과 다를 것이 없음. But, 모든 선택지를 고려해 보고 그중 전체 답이 가장 좋은 것을 찾는 두 방법과는 달리, 탐욕법은 각 단계마다 지금 가장 좋은 방법만을 선택
- 지금의 선택이 앞으로 남은 선택들에 어떤 영향을 끼칠지는 고려하지 않음
- 탐욕법은 많은 경우 최적해를 찾지 못해 사용되는 경우는 크게 두 가지로 제한
- 1.탐욕법을 사용해도 항상 최적해를 구할 수 있는 문제를 만난 경우 -> 탐욕법은 동적 계획법보다 수행 시간이 훨씬 빠름
- 2.시간이나 공간적으로 인해 다른 방법으로 최적해를 찾기 너무 어렵다면 최적해 대신 적당히 괜찮은 답(근사해)을 찾는 것으로 타협 -> 최적은 아니지만 임의의 답보다는 좋은 답을 구하는 용도로 유용 (이 경우는 조합 탐색이나, 메타휴리스틱 알고리즘들이 더 좋은 답을 주는 경우가 많음)
- 문제 추가
Bit-mask
- 비트마스크 : 정수의 이진수 표현을 자료 구조로 쓰는 기법
- 더 빠른 수행 시간
- 더 간결한 코드
- 더 작은 메모리 사용량
- 연관 배열을 배열로 대체
- 용어 정리
- 비트(bit) : 0 혹은 1의 값을 가지고, 컴퓨터가 표현하는 모든 자료의 근간
- 비트 연산자 : 비트마스크를 사용하기 위해서는 정수 변수를 비트별로 조작할 수 있는 비트 연산자를 사용(AND, OR, XOR, NOT, shift)
- 유의 사항
- 우선순위 : c++, java에서는 &, ^ 등의 비트 연산자의 우선순위는 == 혹은 != 등의 비교 연산자보다 낮음 -> 비트마스크 사용 식에 가급적 괄호는 자세하게 추가하는 습관이 중요
- 오버플로 : c++에서 1은 부호 있는 32비트 상수로 취급되므로, shift 연산이 32이상 되어버리면 오버플로가 발생. 정수 뒤에 64비트 정수임을 알려주는 접미사 ‘ull’을 붙여주어야 함. -> 변수의 모든 비트를 다 쓰고 싶을 때는 부호 없는 정수형을 쓰는 것이 좋음
- 집합 구현
- 공집합 : 상수 0
- 꽉 찬 집합 : 100000.. 으로 이루어진 이진수에서 1을 빼면 모든 비트가 켜지게 됨
// 비트가 모두 켜진 수 int full = (1<<20) - 1; // 원소 추가 toppings |= (1 << p); // p = topping number // 원소 삭제 toppings -= (1 << p); // 이미 토핑 목록에 있을 경우 toppings &= ~(1 << p); // 토핑이 없을 경우에도 정상적으로 동작 // 원소 포함 여부 확인 if(toppings & (1 << p)); // 토글 : 해당 비트가 켜져 있으면 끄고, 꺼져 있으면 켜기 toppings ^= (1 << p); // 집합에 포함된 원소의 크기 // c++ 내장 명령어(32비트 부호 없는 정수) : __popcnt(toppings) int bitCount(int x) { if(x == 0) return 0; return x % 2 + bitCount(x/2); // 2^0 + bitCount(x >>1) } // 최소 원소 찾기("이 정수의 이진수 표현에서 끝에 붙은 0이 몇 개인가"에서 착안) // c++ 내장 명령어(32비트 부호 없는 정수) : __BitScanForwatd(&index, toppings) // 최하위 비트의 번호 대신 해당 비트를 직접 구하기 int firstTopping = (toppings & -toppings); // 최소 원소 지우기(어떤 정수가 2의 거듭제곱 값인지 확인할 때 유용) topping &= (toppings -1); // 모든 부분 집한 순회 for(int subset = pizza; subset; subset = ((subset-1) & pizza)) { // subset은 pizza의 부분집합 // for문은 subset = 0인 시점에 종료, 공집합은 방문하지 않음 }
참고
- c++ bitset 클래스 (링크)
Tree
Segment Tree
- 참고
- 구간 트리 : 구간에 대한 질문 대답하기
- 저장된 자료들을 적절히 전처리해 그들에 대한 질의들을 빠르게 대답할 수 있도록 함
- 흔히 일차원 배열의 특정 구간에 대한 질문을 빠르게 대답하는데 사용
- 루드 노드를 배열의 1번 원소로, 노드 i의 왼쪽 자손과 오른쪽 자손을 각각 2 x i 와 2 x i + 1 번 원소로 표현
- 높이는 log2N의 올림이고, 세그먼트 트리를 만드는데 필요한 배열의 크기는 2^(H+1) - 1
- 패턴
long long init(vector<long long> &a, vector<long long> &tree, int node, int start, int end) { if (start == end) { return tree[node] = a[start]; } else { return tree[node] = init(a, tree, node*2, start, (start+end)/2) + init(a, tree, node*2+1, (start+end)/2+1, end); } } void update(vector<long long> &tree, int node, int start, int end, int index, long long diff) { if (index < start || index > end) return; tree[node] = tree[node] + diff; if (start != end) { update(tree,node*2, start, (start+end)/2, index, diff); update(tree,node*2+1, (start+end)/2+1, end, index, diff); } } long long sum(vector<long long> &tree, int node, int start, int end, int left, int right) { if (left > end || right < start) { return 0; } if (left <= start && end <= right) { return tree[node]; } return sum(tree, node*2, start, (start+end)/2, left, right) + sum(tree, node*2+1, (start+end)/2+1, end, left, right); } int main() { ... vector<long long> a(n); int h = (int)ceil(log2(n)); int tree_size = (1 << (h+1)); vector<long long> tree(tree_size); ... return 0; }Fenwick Tree
- 참고1
- 참고2
- 펜윅 트리 혹은 이진 인덱스 트리(binary indexed tree)
- 구간 합 대신 부분 합만을 빠르게 계산할 수 있는 자료구조를 만들어도 구간 합을 계산할 수 있는 알고리즘
- n개의 수에 대한 부분 합을 n개의 숫자에 저장
- 다른 부분합에 대해서 오른쪽 끝 위치의 이진수 표현에서 마지막 비트를 지우면 다음 구간을 쉽게 탐색
- 맨 오른쪽에 있는 1인 비트를 스스로에게 더해 주는 연산을 반복하면 해당 위치를 포함하는 구간들을 모두 만날 수 있음
- 계속 변하는 배열의 구간 합을 구할 때는 구간 트리보다 펜윅 트리를 자주 사용
- 패턴
long long sum(vector<long long> &tree, int i) { long long ans = 0; while (i > 0) { ans += tree[i]; i -= (i & -i); } return ans; } void update(vector<long long> &tree, int i, long long diff) { while (i < tree.size()) { tree[i] += diff; i += (i & -i); } } int main() { ... vector<long long> a(n+1); vector<long long> tree(n+1); ... }Graph
- 그래프 G(V, E)는 어떤 자료나 개념을 표현하는 정점(vertex)들의 집합 V와 이들을 연결하는 간선(edge)들의 집합 E로 구성된 자료 구조
- 그래프의 종류
- 방향 그래프(directed graph) or 유향 그래프 : 각 간선이 방향이라는 새로운 속성을 갖음
- 무향 그래프(undirected graph) : 간선에 방향이 없는 그래프
- 가중치 그래프(weighted graph) : 각 간선에 가중치(weight)라고 불리는 실수 속성을 부여
- 다중 그래프(multi graph) : 두 정점 사이에 두 개 이상의 간선이 있을 수 있는 그래프
- 단순 그래프(simple graph) : 두 정점 사이에 최대 한 개의 간선만 있는 그래프
- 트리 or 루트 없는 트리(unrooted tree) : 부모 자식 관계가 없을 뿐, 간선들의 연결 관계만 보면 트리와 같은 무향 그래프
- 이분 그래프(bipartite graph) : 그래프의 정점들을 겹치지 않는 두 개의 그룹으로 나눠서 서로 다른 그룹에 속한 정점들 간에만 간선이 존재하도록 만들 수 있는 그래프
- 사이클 없는 방향 그래프(directed acyclic graph), DAG : 가중치 그래프 + 이분 가중치 그래프, 방향 그래프인데 한 점에서 출발해 자기 자신으로 돌아오는 경로(cycle)가 존자해지 않는 경우
- 그래프의 경로(path)
- 그래프에서 사용되는 가장 중요한 개념
- 끝과 끝이 서로 연결된 간선들을 순서대로 나열한 것
- 뱡향 그래프의 경우, 앞 간선의 끝점이 뒷 간선의 시작점과 만나야 함
- 단순 경로(simple path) : 경로 중 한 정점을 최대 한 번만 지나는 경로
- 사이클(cycle) or 회로 : 시작한 점에서 끝나는 경로
그래프의 표현 방법
- 많은 경우 트리에 비해 훨씬 정적인(새로운 정점, 간선 변경이 적음) 용도로 사용
- 구조의 변경이 어렵지만 더 간단하고 메모리를 적게 차지하는 방법으로 구현
인접 리스트 표현
그래프의 각 정점마다 해당 정점에서 나가는 간선의 목록을 저장해서 그래프를 표현
vector<list<int>> adjacent; // 가중치 그래프 등 간선이 추가적 속성을 갖는 그래프를 표현 struct Edge { int vertex; // 간선의 반대쪽 끝 점의 번호 int weight; // 간선의 가중치 }; // 위 구조체를 단순하게 pair class 를 사용해도 무방 pair<int, int> 로 사용- 단점으로 두 정점이 주어질 때 이 정점이 연결되어 있는지 알기 위해 연결 리스트를 일일이 뒤져야 함
인접 행렬(adjacency matrix) 표현 방식
인접 리스트의 연산 속도를 높이기 위해 고안된 그래프 표현 방식
2차원 배열을 이용해 그래프의 간선 정보를 저장
vector<vector<bool>> adjacent;- 두 정점 사이에 간선이 없는 경우에는 이 값을 -1 혹은 아주 큰 값 등 존재할 수 없는 값으로 지정
인접 행렬 표현과 인접 리스트 표현의 비교
- 희소 그래프(sparse graph) : 간선의 수가 fabs(V)^2 에 비해 훨씬 적은 그래프일 경우 인접 리스트를 사용하는 것이 유리
- 밀집 그래프(dense graph) : 간선의 수가 거의 fabs(V)^2 에 비례하는 그래프일 경우 인접 행렬을 사용하는 것이 유리
References
알고리즘 문제 해결 전략, 구종만, 인사이트(2012)